Leren vermenigvuldigen is een cruciaal onderdeel van het rekenonderwijs in de basisschool. Malmberg heeft een duidelijke visie op hoe kinderen deze vaardigheid het beste kunnen ontwikkelen: namelijk een duidelijke opbouw van begrip en het aanleren van strategieën, in plaats van beginnen met het stampen van de tafels. Wij leggen uit waarom.
1×2=2. 2×2=4. 3×2=6… Heb jij als kind ook de tafels moeten opdreunen in de klas? Maar begreep je eigenlijk wel wat je opdreunde? Leren vermenigvuldigen draait o.a. om het eerst begrijpen wat vermenigvuldigen is. En om hoe je een keersom uitrekent: welke strategie kan ik het beste gebruiken? Pas als je dat goed begrepen hebt, kun je verder met het vlot leren uitrekenen van de tafels en met het uit je hoofd leren van de tafels. Deze opbouw staat in de rekenmethodes van Malmberg centraal – mét effect!
Sterke basis
De leerlijn vermenigvuldigen bij Pluspunt en bij De wereld in getallen is opgebouwd volgens de 4 fasen van het hoofdfasenmodel. Het hoofdfasenmodel is één van de modellen uit het ERWD-protocol (Van Groene, Borghouts & Janssen, 2011). De kern van dit model is dat elke volgende fase in de leerlijn uitgaat van beheersing van de voorafgaande fase (Borghouts, 2015). Om tot automatiseren van alle tafels te komen -doel eind groep 4 – moeten de fasen begripsvorming en procedureontwikkeling in orde zijn.
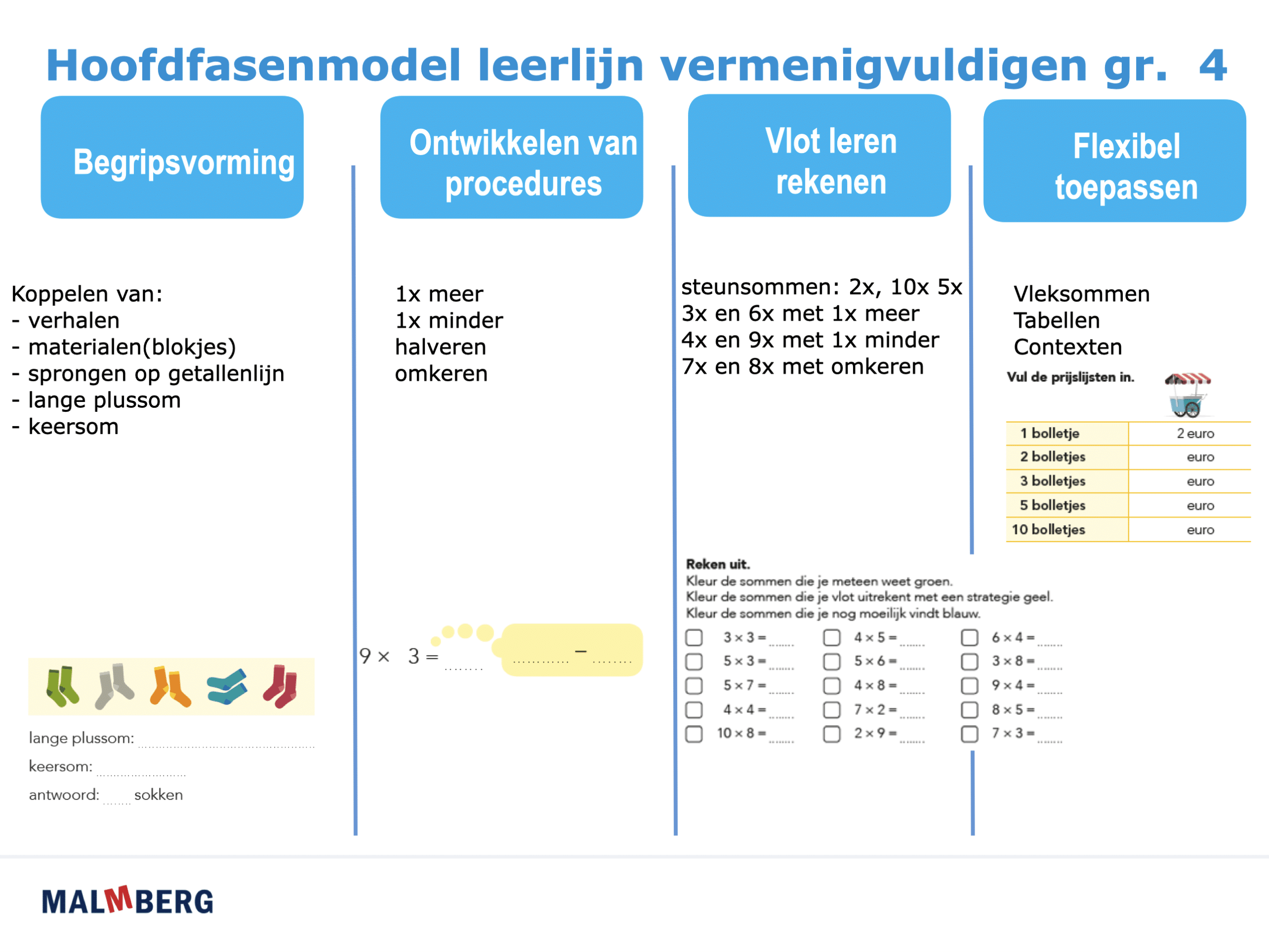
Fase 1: begripsvorming
Bij de begripsvorming gaat het om conceptontwikkeling en betekenisverlening. Dit is de basis voor elke leerlijn. Het begrijpen van rekenwiskundige concepten is het fundament van een goede rekenontwikkeling. Wanneer de basis niet goed is, zal het bouwwerk wankel zijn. Bij begripsvorming vermenigvuldigen gaat het om betekenisverlening en reflectie voor elke keersom. De kinderen maken de koppeling tussen een verhaal, tekening, materiaal, getallenlijn, de lange plussom en de keersom Ze snappen wat de getallen uit de som betekenen in relatie tot het verhaal.
Een voorbeeld bij de som 3 × 6 = 18
Bij het verhaal ‘Er zitten 6 koeken in een pak, ik koop 3 pakken, hoeveel koeken heb ik dan?’ zelfstandig de juiste keersom kunnen bedenken:
- begrijpen wat de getallen 3, 6 en 18 in die som betekenen in relatie tot het verhaal;
- dat verhaal kunnen laten zien met blokjes;
- dat verhaal kunnen schetsen:

- dat verhaal kunnen tekenen op de getallenlijn:
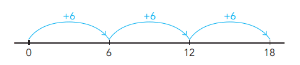
- dat verhaal kunnen weergeven in een lange plussom: 6+6+6=18;
Dit is voor alle tafelsommen hetzelfde.
Fase 2: Ontwikkelen van procedures
Als de leerlingen de fase van begripsvorming hebben afgerond, gaan ze strategieën ontwikkelen. Er wordt niet per tafel gewerkt. Eerst leren de kinderen van alle tafels 3 steunsommen: 10x, 5x en 2x. De steunsom 5x leren ze via de strategie halveren. Let op: Deze steunsommen zijn dus niet hetzelfde als de tafels van 2, 5 en 10. Het gaat bijvoorbeeld om de steunsom 2x van elke tafel, dus 2×1, 2×2, 2×3 etc.
Het is belangrijk om veel tijd te besteden aan het memoriseren (gelijk het antwoord uit het hoofd weten) van deze steunsommen. Deze steunsommen zijn namelijk het uitgangspunt bij het gebruik van de strategieën 1x meer en 1x minder. Hiermee kunnen de kinderen 3x (1x meer dan 2x), 4x (1x minder dan 5x), 6x (1x meer dan 5x) en 9x (1x minder dan 10x) uitrekenen. De omkeerstrategie wordt gebruikt voor de 7x en 8x sommen van alle tafels. Met deze strategieën kunnen kinderen bijna alle tafelsommen uitrekenen. Er blijven slechts een paar tafelsommen over zoals: 7×7, 7×8, 8×8 en 8×7. Deze moeten extra geoefend worden.
Fase 3: Vlot leren rekenen en automatiseren
Automatiseren van vermenigvuldigen is een belangrijk onderdeel van het rekenonderwijs. Bij automatiseren gaat het om het vlot en correct iets kunnen uitrekenen met efficiënt strategiegebruik.
Kort samengevat kom je bij het leren van de tafels tot automatiseren door:
- de steunsommen te kennen (10x, 5x, 2x). Oefen deze vaak!
- de strategieën 1x meer, 1x minder en omkeren te begrijpen en beheersen
- het optellen en aftrekken t/m 100 te beheersen
Als leerlingen problemen hebben met het bovenstaande dan gaat het automatiseren van de tafelsommen niet lukken. Het heeft dan ook geen zin om ze extra te laten oefenen op snelheid, wat helaas vaak op scholen gebeurt. Het is van belang om eerst te observeren of de steunsommen, de strategieën en het rekenen t/m 100 beheerst worden. Een aantal bouwstenen uit de leerlijn optellen en aftrekken t/m 100 is namelijk voorwaardelijk om succesvol de tafels te kunnen leren: bijvoorbeeld het aftrekken van een tiental (60-6), maar ook sommen als 35+7 en 35-7 vlot in 2 stappen via het tiental kunnen uitrekenen. Deze sommen zijn voorwaardelijk bij het toepassen van de strategieën 1x meer en 1x minder. Bij beheersing van deze vaardigheden kan gestart worden met automatiseren. Bij het automatiseren gaat het dan om vlot de strategieën toepassen, herkennen welke strategie je kunt gebruiken en wanneer.
Begin je te vroeg, dan leert het kind de strategieën niet, wat verderop in de leerlijn tot grote problemen kan leiden!
Om bovenstaande redenen wordt in de rekenmethodes van Malmberg het automatiseren van de tafels aangeboden vanaf de tweede helft van groep 4. Begin je te vroeg met automatiseren en met het stampen van tafels, als een kind de vaardigheden nog niet beheerst, dan is de kans groot dat het kind steeds tot een antwoord komt door herhaald optellen. Zo leert het kind de strategieën niet, wat verderop in de leerlijn tot grote problemen kan leiden!
Na het automatiseren volgt de noeste arbeid, het memoriseren. In groep 5 moeten alle tafels gememoriseerd zijn. Om variatie in oefening aan te brengen bij het automatiseren, memoriseren en bij het onderhouden van de tafels, kunnen er verschillende spellen gebruikt worden, zie hiervoor de katernen Spelenderwijs leren rekenen bij Pluspunt 4 en De wereld in getallen 5.
Fase 4: Breed en flexibel toepassen
In deze fase kan het kind de juiste keersom uit de context (verhaal, foto, etc.) halen. Het gaat uiteindelijk om het kunnen toepassen van de kennis. Deze opbouw van de leerlijn vermenigvuldigen m.b.v. het hoofdfasenmodel versterkt het wiskundig inzicht en maakt kinderen zelfredzaam. Bovendien draagt deze aanpak bij aan het zelfvertrouwen van leerlingen. Dit verlaagt faalangst en verhoogt de motivatie om te leren.
Begrip, flexibiliteit en inzicht
Effectief rekenonderwijs draait om begrip, flexibiliteit en inzicht. Door te starten met conceptueel leren en geleidelijk over te gaan naar automatiseren, ontwikkelen kinderen niet alleen rekenvaardigheid, maar ook een stevige basis voor toekomstig succes. Leerkrachten die met de rekenmethodes van Malmberg werken, zien dat kinderen niet alleen met meer begrip leren, maar ook meer plezier hebben in het proces. En dat is precies wat goed onderwijs beoogt!
Literatuur
Borghouts, C. , (2015 eerste druk). Voorkom (ernstige) rekenproblemen. Dordrecht: TIB, Instondo BV.
Groenestijn, M. van e.a. (2011). Protocol Ernstige RekenWiskunde-problemen en Dyscalculie (ERWD). Assen: Van Gorcum