‘Toen ik op de middelbare school zat, had ik veel moeite met de vakken natuurkunde en wiskunde. Ik zag daar geen aansluiting met de werkelijkheid. Ik zette door, want ik wilde bioloog worden en dan had je beide genoemde vakken nodig. Tijdens mijn studie en later toen ik leraar werd, begon ik de waarde van deze vakken te begrijpen en vooral voor mijn eigen vak.’
Dit vertelt René Westra, jullie welbekende toetsen-expert en biologiedocent. Hij maakte een knaller van een opdracht, met wel 3 video’s om te bekijken en bijpassende vragen. Veel plezier en succes!
Begin met de film ‘ 3/4 Kleibers Law’:
Je zag dat de Amerikaanse onderzoeker en dierenarts Max Kleiber wiskundige formules ontwikkelde over het energiegebruik van dieren. Ze staan hieronder:
Rh = 4.1 x M0.75
Rp = 0.14 x M0.75
Hierin is: R de ‘metabolic Rate’ of basale stofwisselingssnelheid (in Watts = J/sec), dat is dus de snelheid van de stofwisseling in rust. M is de massa van een dier (in kg), h een index voor homoiotherm (dier met constante lichaamstemperatuur) en p een index voor poikilotherm (dier met variabele lichaamstemperatuur).
Een natuurkundige zou, door te kijken naar de toepassing van de schaalregel op dieren van toenemende massa (via de verhouding oppervlak: inhoud), uitkomen op een exponent van 0,67. Immers, het oppervlak neemt toe met een kwadratische functie, de inhoud met een derde machtsfunctie, dus hun verhouding met een exponent 2/3 = 0,67. Maar Kleiber ontdekte via praktisch onderzoek in 1932 dat de massa-exponent in alle diergroepen 0,75 is. Door biologische aanpassingen is de exponent in de praktijk hoger dan de natuurkunde voorspelt. Hierdoor zal een klein dier relatief minder warmte verliezen en een minder intensieve stofwisseling nodig hebben.
Vragen (deel 1)
1. Geef een voorbeeld van een poikilotherm dier en leg uit dat dit dier een veel lagere stofwisselingssnelheid heeft dan een even zwaar homoiotherm dier. Geef ook daarvan een voorbeeld.
2. Frank en John slapen allebei 8 uur. Frank weegt 60 kg, John 80 kg. Bereken de basale stofwisselingssnelheid van beiden.
3. Leg met een berekening uit dat John meer voedsel bij zijn ontbijt nodig heeft dan Frank.
Bekijk nu de film ‘De gulden snede en de spiraal’.
De gulden snede is dus het getal (ook wel aangeduid met het symbool φ) dat je terugvindt bij rechthoeken. De rechthoek met zijden a en b, die overblijft na verwijdering van het vierkant met zijde a, is gelijkvormig met de oorspronkelijke rechthoek.
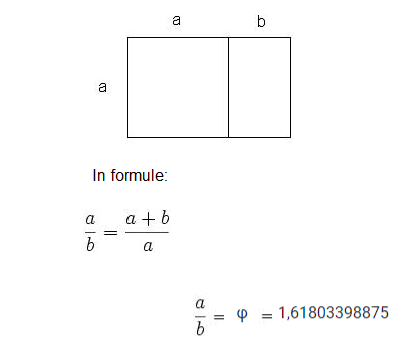
De Gulden snede geeft een verhouding weer die vaak in de natuur wordt aangetroffen.
Vragen (deel 2)
4. Welk getal vind je (afgerond op 3 cijfers achter de komma) als je de lengte van je onderarm (a) deelt door de lengte van je hand (b)? Zet je uitkomst op het bord en vergelijk jouw uitkomst met die van je klasgenoten. Wat valt je op?
5. Doe eenzelfde meting en verwerking voor de lengte van je hoofd (a) gedeeld door de breedte van je hoofd (b).
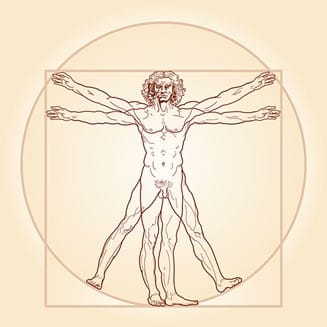
Tijdens de Europese Renaissance gebruikten gerenommeerde kunstenaars en architecten de gulden snede om hun meesterwerken in kaart te brengen. Daarnaast waren zij geïnteresseerd in symmetrie. Dat betekent in een formule dat a = b. Bijvoorbeeld het rechterbeen is even lang als het linkerbeen en het rechteroog ligt even ver van de rand van het gezicht als het linkeroog.
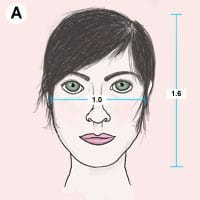
Sommige wetenschappers hebben de wiskundige formule van de gulden snede en gegevens van symmetrie gebruikt om te helpen verklaren waarom sommige mensen door veel andere mensen als mooi worden beschouwd, hoewel het begrip mooi natuurlijk niet echt objectief is te bepalen.
Zo gebruikte Dr. Kendra Schmid, een assistent-professor in de biostatistiek, de gulden snede en metingen aan symmetrie om ‘sex appeal’ in het gezicht te bestuderen. Om te beginnen mat ze de lengte en breedte van het gezicht. Daarna mat ze drie segmenten van het gezicht: van de haarlijn van het voorhoofd tot een plek tussen de ogen, van tussen de ogen tot de onderkant van de neus en van de onderkant van de neus tot de onderkant van de kin. Als de getallen gelijk zijn, wordt een persoon als mooier beschouwd.

Tenslotte mat ze nog enkele gelaatstrekken om symmetrie en proportie te bepalen. Over een perfect gezicht zegt Dr. Schmid dat de lengte van een oor gelijk is aan de lengte van de neus, en de breedte van een oog is gelijk aan de afstand tussen de ogen.
Uit dergelijke metingen bleek Amber Heard van een groot aantal gemeten filmsterren “de mooiste”. Een schrale troost na het door haar verloren proces met Johnny Depp.
In de sport is een verhouding van lichaam en lichaamsdelen, met perfecte gulden snede- en symmetriewaarden, zoals te zien in de afbeelding van Michelangelo, niet altijd ideaal. Lange armen zijn soms een voordeel, zoals bij roeien of zwemmen.
Bekijk nu de video ‘The Ape index and your climbing potential’.
Vragen (deel 3)
Hier gebruikt men de zogenaamde aapfactor. De aapfactor is de verhouding tussen de spanwijdte van de armen ten opzichte van de lichaamslengte.

Bij roeien kun je voor sporters met een lage aapfactor nog corrigeren via de afstelling van de riemen (zoals bleek bij skiffeuse Karolien Florijn, die met een aapfactor van precies 1 toch met lengtes voorsprong Europees skiffkampioen werd). Maar bij zwemmen, discuswerpen of basketballen zijn sporters met lange armen (dus met een aapfactor van boven de 1) echt in het voordeel.

Bij een mensaap zoals de orang oetan is die factor 1,2 en bij de meeste mensen ongeveer 1,0 (zoals in de tekening van Michelangelo). Maar bijvoorbeeld bij de Amerikaanse zwemmer Michael Phelps, die drieëntwintig gouden medailles won op de Olympische Spelen, is die factor 1,05.
En de Litouwse discuswerper Mykolas Alekna (links), die in april 2024 het stokoude wereldrecord uit 1986 verbeterde, heeft een spanwijdte van 220 cm en een lichaamslengte van 201 cm.
Laatste vragen
6. Aapfactor is eigenlijk een verkeerde vertaling van het Engelse ape factor. Leg dit uit.
7. Wat is de aapfactor van Alekna?
8. Noem een ander kenmerk dat naast een hoge aapfactor bepalend is voor een goede klimcapaciteit.
9. Bepaal volgens de bovenste formule met behulp van een duo-partner en een meetlint jouw aapfactor. Vergelijk die met je klasgenoten. Net als bij veel andere zaken (bijvoorbeeld proefwerkcijfers) zul je merken dat er bij alles wat je in deze opdracht meet, variatie aanwezig is.
10. In de evolutietheorie is variatie een heel belangrijk onderdeel. Leg dit uit.
11. Bij gewichtheffen moet de atleet bij het trekken een halter in één vloeiende beweging met gestrekte armen tot boven het hoofd brengen. Leg uit dat bij deze oefening juist een lage aapfactor gunstig is.
Antwoorden bekijken
Om de antwoorden te kunnen zien, moet je zijn ingelogd. Heb je nog geen account? Meld je dan nu aan! Het is GRATIS.